ChLaLoRoSa06.dvi

new functions extend the conventional PC architecture by
mechanisms to (i) protect cryptographic keys, (ii) generate
random numbers in hardware, (iii) cryptographically bind
(sensitive) data to certain information, e.g., the system con-
figuration and the identifier of the invoking application (

seal-

ing

), and (iv) authenticate a platform/application

(remote

attestation)

The TCG solution for platform authentication is some-

times called

binary attestation

, since loosely speaking, it

measures all the code executed by using certain metrics (cur-
rently a cryptographic hash value over the code binary). The
result is stored in special registers in the TPM before execut-
ing the code. This procedure is bootstrapped starting with
a kind of pre-BIOS that is trusted by default and measures
the bootloader, storing the result. This procedure builds the
so-called

chain of trust

which can then be extended to the

operating system components up to applications.

Binary attestation, however, has several shortcomings, in

particular for application attestation, regarding flexibility
and security/privacy as pointed out in [27, 29]: First, re-
vealing the system configuration may lead to privacy viola-
tions and discrimination against the underlying system since
the remote party may exclude them from his/her business
model, e.g., configurations related to alternative operating
systems such as Linux. Note that similar approaches can be
observed today, e.g., many banks provide banking software
for only one operating system and some music players expect
a specific operating system. It then reveals the complete in-
formation about the hardware and software configuration of
a platform which makes attacks easier. Second, it requires
the verifier to know all possible “trusted” configurations of
all platforms.

Third, it does not necessarily imply that the

platform complies with desired (security) properties.

In contrast to binary attestation, a more general and flex-

ible solution is to use

property-based attestation

to attest

properties of the underlying platform or/and application in-
stead of revealing the binary information about them. Loose-
ly speaking, a

property

of a platform describes an aspect

of the behavior of that platform regarding certain require-
ments, such as security-related requirements (e.g., that a
platform has built-in measures for Multilevel Security or pri-
vacy protection, or it has a security kernel providing isola-
tion of applications). Attesting properties means that the
attestation should only determine whether a platform (or its
configuration) fulfills a desired property, instead of revealing
the concrete configuration of its software and hardware com-
ponents. Attesting properties has the advantage that differ-
ent platforms with different components may have different
configurations while they may all offer the same properties
and consequently fulfill the same requirements. In particu-
lar, this solution also allows a more flexible way of handling
system patches and updates.

In this context it is important one needs to define which

properties are useful and reasonable, and how to determine
them automatically. The former depends strongly on the
underlying use case and its requirements and the latter may

Other problems related to attestation are updates/patches

and backup: the new functionalities allow to seal critical
data (e.g., documents, content) to a certain platform config-

uration. This, however, strongly limits the flexibility when
system updates (e.g., patches) change the system configura-
tion. As a consequence, the data is not accessible anymore.
Similar situations arise with system backups.

be performed in different ways in practice as we briefly con-
sider in Section 5.1.

Our proposal for property-based attestation in this paper

is based on the ideas in [29], where the authors informally
discuss several solutions which differ in their trust mod-
els, efficiency and the functionalities offered by the trusted
components. We will consider other related works in Sec-
tion 2.

The core idea presented in [29] is what we call

delegation-based

property attestation. Here, a certification

agency certifies the mapping between properties and con-
figurations and publishes these

property certificates

. After

this, the agency remains completely offline. Now a plat-
form/application claiming to provide a certain property can
download the appropriate certificate(s), and prove to any
(correct) verifier that it has a valid certificate, since its con-
figuration matches the one fixed in the property certificate
without disclosing any information about the content of the
certificate (except the property which is a common input
which is public by definition). In particular, we are inter-
ested in TCG compliant solutions allowing to use TSS and
the existing TC hardware without a need to change the un-
derlying trust model of TCG.

Our contribution.

We propose a provably secure protocol

for property-based attestation that concretely implements
the delegation-based solution sketched above. Our solution
is based on the current TCG specification, because today
it is the most widely known and available extension of con-
ventional computer systems that provides the measurement
and attestation of integrity metrics. Hence, our scheme uses
a hybrid approach where a property attestor (e.g., a ser-
vice of a security kernel) calls on a binary attestor (here
the TPM). Our scheme allows the revocation of invalid con-
figurations either from a public list or negotiated between
the prover (platform) and a verifier. The deployed crypto-
graphic schemes are based on CL signatures [6] and signa-
ture proofs of knowledge similar to those in DAA [4]. The
property revocation protocol is based on [7].

RELATED WORK

There have been several proposals in the literature for

protecting and proving the integrity of computing platforms
based on cryptographic techniques and trusted components.
Known aspects in this context are secure and authenticated
(or trusted) booting: the former means that a system can
measure its own integrity and terminates the boot process
in case the integrity check fails, whereas the latter aims at
proving the platform integrity to a (remote) verifier (for both
topics see, e.g., [1], [11]).

In [29], and later in [27], the authors propose an approach

called

property attestation

to prevent the deficiencies of the

existing binary attestation. The basic idea in [27] is to en-
gage a protocol between verifier and attestor to prove that
the attested platform satisfies the verifier’s security require-

It should be noted that our primary goal is to have a

non-discriminating attestation as a standard, which can

be certified by trusted entities, and on which the vendors
and developers of related products should rely.

Clearly,

standards leave some space for corresponding implemen-

tations, and this may open the door for information flow
allowing, e.g., operating system footprinting (see, e.g.,
www.insecure.org/nmap). However, this is not the subject
of this paper.

ments. Their solution is based on property certificates that
are used by a

verification proxy

to translate binary attesta-

tions into property attestations. Moreover, this work briefly
discusses two deployment scenarios: The verification proxy
as a dedicated machine and the verification proxy on the
verified platform. Whereas [27] proposes a high-level pro-
tocol for property-based attestation, [29] proposes and dis-
cusses several protocols and mechanisms that differ in their
trust models, efficiency and the functionalities offered by the
trusted components.

The authors of [16] propose

semantic remote attestation

– using language-based trusted virtual machines (VM) to
remotely attest high-level program properties. The general
idea behind this approach is the use of a trusted virtual
machine that checks the security policy of the code that runs
within the VM. Since the trusted VM still has to be binary
attested, semantic remote attestation is a hybrid solution
with code analysis.

In [18], [20], and [19] the authors propose a software ar-

chitecture based on Linux providing attestation and sealing.
The architecture allows to bind short-lifetime data (e.g., ap-
plication data) to long-lifetime data (e.g., the Linux kernel)
and to allow access to the data only if the system is com-
patible with a security policy certified by a security adminis-
trator. Moreover, these papers suggest to use a certification
authority that certifies the trustworthiness of certain config-
urations of long-lifetime data. Thus, the proposed architec-
ture is very similar to a hybrid approach based on property
certificates as we use in this paper.

TCG MAIN COMPONENTS

The core specification of Trusted Computing Group (TCG)

concerns the Trusted Platform Module [36, 35], a compo-
nent which provides certain cryptographic functions. The
assumption is that this party is fully trusted. The current
implementation of the TPM is a tamper-evident hardware
chip. Other major components of the TCG proposal are
a kind of (protected) pre-BIOS (Basic I/O System) called
the

Core Root of Trust for Measurement

(CRTM), and a

support software called

Trusted Software Stack

(TSS) which

performs various functions like communicating with the rest
of the platform or with other platforms.

Trusted Platform Module & Platform Configura-
tion

A TPM provides a secure random number genera-

tor, non-volatile tamper-resistant storage, key generation
algorithms, and cryptographic functions for encryption/de-
cryption, digital signatures (RSA) and a cryptographic hash
function (SHA-1).

Moreover, the TPM includes a set of registers called

Plat-

form Configuration Registers

(PCR) which can be used to

store hash values.

Integrity Measurement

The so-called

Integrity Measure-

ment

is done during the boot process by computing a crypto-

graphic hash of the initial platform state. For this purpose,
the CRTM computes a hash of (“measures”) the code and
parameters of the BIOS and extends the first PCR register
by this result according to

PCR

←

SHA1(

PCR

Input).

chain of trust

is established, if, additionally, both BIOS

and bootloader measure the code they are executing as well.
Hence,

PCR

, . . . ,

PCR

provide evidence of a certain state

of the system immediately after the boot process, which we
define as the platform’s

configuration specification

, denoted

abstractly by

:= (

PCR

, . . . ,

PCR

Attestation

The TCG attestation protocol is used to give

assurance about the platform configuration

to a remote

party. Here the attesting party, the

attestor

, reports to a

remote party, the

verifier

, the configuration of a machine(s)

to be attested, e.g., the configuration of the platform or/and
of applications. To guarantee integrity and freshness, this
value and a fresh nonce

must be digitally signed with an

asymmetric key called

Attestation Identity Key

(AIK) that

is under the sole control of the TPM. A trusted third party
called

Privacy Certification Authority

(Privacy-CA) is used

to guarantee the pseudonymity of the AIKs. However, this
party can always link the transactions a certain platform was
involved in. To overcome this problem, version 1.2 of the
TCG specification [35] defines another cryptographic pro-
tocol called

Direct Anonymous Attestation (DAA)

[4] that,

roughly spoken, provides users with an unlimited number of
pseudonyms without requiring a Privacy-CA. Note that the
anonymity provided by DAA or Privacy-CAs is completely
orthogonal to the stated goals of this paper. Nevertheless,
we will show in Section 7 how both approaches can be com-
bined into an (unlinkable) property-based attestation func-
tion.

TCG (implicit) Assumptions

The functionality men-

tioned above is provided based on the following assumptions:
First, the platform configuration cannot be overwritten af-
ter measurements (i.e., after the hash values are computed
and securely stored in the TPM). Since the TCG makes
statements about the initial state of the platform only, it is
crucial that this state cannot be (maliciously) manipulated
after startup, otherwise a verifier cannot rely on the informa-
tion provided by the attestor. However, currently available
operating systems (e.g., Windows, Linux) can easily be ma-
nipulated by exploiting security bugs or by changing mem-
ory which has been swapped to a harddisk. Second, given a
valid set of hash values, the challenger is able to determine
whether the platform configuration is trustworthy. However,
the trusted computing base of today’s operating systems is
very complex, making it very hard, if not impossible, to de-
termine their trustworthiness. Third, the following secure
channels can be established: (i) between hardware compo-
nents (e.g., between TPM and CPU) since both components
are integrated on the same hardware;

(ii) between the at-

testor and the verifier, which can reasonably be achieved by
a public key infrastructure (PKI) [35], and (iii) between the
attestor and the attested machine, which should be provided
by the underlying operating system.

Hence, a secure operating system is required that (i) ef-

fectively prevents unauthorized modifications, (ii) is small
enough to allow an evaluation of its trustworthiness, (iii)
provides secure interprocess communication mechanisms, and

Here we do not mean the hash value of the history but

rather the hash of the TCB (Trusted Computing Base) state

that remains unchanged during the run-time in contrast to,
e.g., history measurements done in [34].

Experience shows that this assumption does not hold for

the currently available TPM platforms, since it is possible
to observe resp. modify the communication between CPU
and TPM.

(iv) last but not least, it should be compatible to the legacy
software. The recent development in the field of security
kernel design (based on e.g., hypervisors or microkernels)
shows that these properties can be efficiently provided (see,
e.g., [25, 28, 12] and [33, 32, 2, 3]).

DEFICIENCIES OF TCG ATTESTATION

As already mentioned in the introduction, while the at-

testation (and sealing) mechanisms provided by the TCG
allow many interesting applications (see, e.g., [31, 14, 17,
34]), the naive use of the platform configuration (e.g., to
bind short-term data to platforms or to determine the trust-
worthiness of applications) has some drawbacks, like the fol-
lowing: the first problem is the potential to be misused for

discrimination

, e.g., to isolate “alternative” software prod-

ucts (e.g., OpenOffice

or WINE

and operating systems

such as Linux). It is imaginable that global players such as
content providers and large operating system vendors col-
laborate and exclude specific operating systems as well as
applications. This barrier to entry effectively undermines
competition and prevents the self-regulating mechanisms of
an open market. The second problem is

complexity

since

the number of different platform configurations grows expo-
nentially with the number of patches, compiler options and
software versions. This makes it hard to keep track of the
trustworthiness of a given configuration. The third prob-
lem is

observability

, since the recipient of the attestation

protocol or an observer obtains exact information about the
hard- and software configuration of a specific platform. This
makes attacks on such platforms much easier since an ad-
versary does not need to perform any platform analysis. A
further problem is the

scalability

, since update and patches

lead to configuration changes.

PROPERTY-BASED ATTESTATION

A more general and flexible solution to the attestation

problem is a

property-based attestation (PBA)

approach [29,

27]. It means that attestation should only determine whether
a platform (configuration) or an application has the desired
property. This avoids revealing the concrete configuration of
software and hardware components. For example, it would
not matter whether the application was Webbrowser

, as long as both have the same properties. In contrast,

the binary attestation function provided by TCG-compliant
hardware attests the system configuration of a platform that
was determined at system startup. For (nearly) all practical
applications, the verifier is not really interested in the spe-
cific system or application configuration. As we pointed out
in Section 4, this even has a disadvantage due to the multi-
tude of possible configurations a verifier has to manage.

Informally, a

property

, in this context, describes an aspect

of the behavior of the underlying object (platform / applica-
tion) with respect to certain requirements, e.g., a security-
related requirement. In general, properties for different ab-
straction levels are imaginable. For instance, a platform
property may state that a platform is

privacy-preserving

i.e., it has built-in measures conform to the privacy laws,
or that the platform provides

isolation

, i.e., strictly sepa-

rates processes from each other, or it provides

Multi-Level

Security

(MLS) and so forth.

www.openoffice.org

www.winehq.org

The question whether there is a correct or useful prop-

erty set depends strongly on the underlying use case and its
requirements. Attesting properties has the advantage that
different platforms with different components may have dif-
ferent configurations while they all may offer the same prop-
erties and consequently fulfill the same requirements.

5.1

Determining Properties

Before the attestor can make statements about a machine,

the appropriate properties have to be determined. We may
group possible mechanisms for determining the properties
of a machine into the following categories such as

code con-

trol

code analysis

delegation

. Code control requires a

trusted attestor enforcing a machine to behave as expected
(e.g., the attestor compares the I/O behavior of the ma-
chine with that defined by the desired property

). An ex-

ample would be to use SELinux as a reference monitor and
to attest both SELinux and the enforced security policy, as
described in [19]. Code analysis requires the property at-
testor to directly analyze the code of the targeted machine
to derive properties, or alternatively, it verifies whether the
machine provides the claimed properties. Examples in this
context are proof-carrying code [23] and semantic code anal-
ysis [16]. The delegation approach requires the property at-
testor to prove that another trusted third party has certified
the desired properties. Obviously, this third party has to be
trusted by both the platform to be attested and the verifier.
A practical example in this context are property certificates
issued by a certificate issuer: The property attestor proves
that a property certificate exists and was issued by a third
party which is trusted by the verifier.

In this paper, we follow the delegation-based approach

with an offline trusted third party. Section 5.2 details this
approach and the underlying abstract model of the system.

5.2

Delegation-Based Solution

In this section, we explain the general idea of the delega-

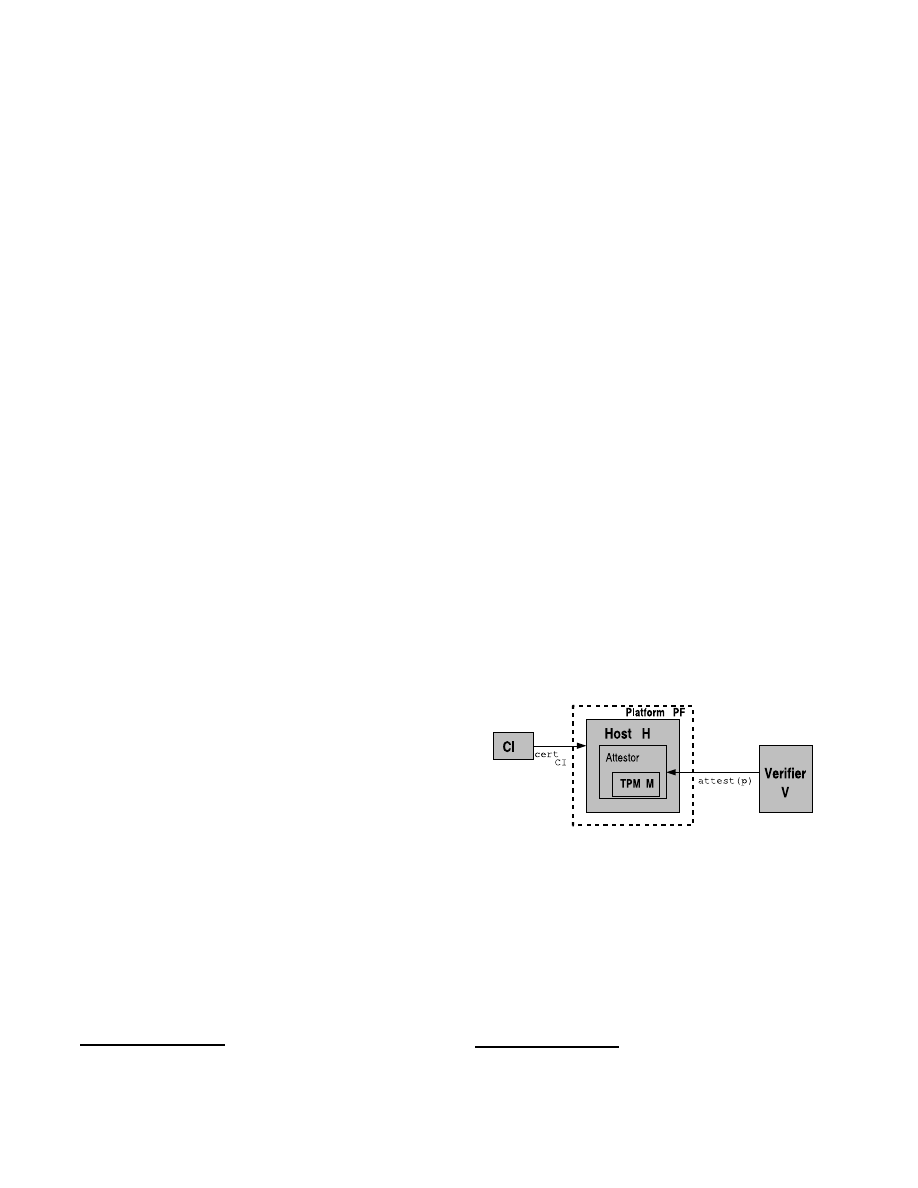
tion-based property-based attestation. Figure 1 illustrates

Figure 1: Abstract model of the attestation scenario
with certificate issuer

, platform

, host

, TPM

and verifier

the abstract model with certificate issuer, platform, host,
attestor, TPM and verifier. In the following, we introduce
the involved roles.

Roles

platform

, denoted by

, represents our main IT

system, i.e., it consists of all (software and hardware) com-
ponents of a system. The

Trusted Platform Module

(TPM)

is denoted by

, and is one of the main components of a

One may consider the desired properties of an application

as a certain input/output behavior.

platform

. The TPM has a predefined set of computa-

tional and cryptographic capabilities (see Section 3) and is
trusted by all parties. A

host

is the other main compo-

nent of

, in which a TPM

is embedded. The host

includes the software running on the platform

. The

TPM can only communicate with other parties (external to
the platform) via the host. A

verifier

is denoted by

and

is a party that wants to verify the attestation result of some
platform. The

certificate issuer

, denoted by

, is the party

that certifies mappings between properties and configura-
tions attesting that a given platform configuration

fulfills

a desired property

by means of a property certificate

(see Figure 1).

Note that for security protocols, such as PBA or DAA,

a trusted component (trusted by the platform or platform
owner) is needed within the host that can establish secure
channels to the attestor.

More precisely, this component

must belong to the Trusted Computing Base (TCB). Oth-
erwise, the host can easily disclose to the verifier the config-
uration of the corresponding platform or/and application in
the context of PBA (or the TPM identity in the context of
DAA).

The delegation-based principle is well-suited to the TCG

trust model and the related infrastructure that already re-
quires trust in third parties (e.g., Privacy-CA, certificate
issuer in the context of DAA, or Migration Authority for
migratable keys [36, 35]). Our approach is a

hybrid attesta-

tion

, which means a two-level chain of attestations, where

the first attestation is based on binary configurations (by
the TPM) and the second one based on properties (by the
corresponding PBA service).

For a general property-based attestation, we assume in

our model that applications are attested by the operating
system. We stress that in this way, we only need to establish
a trusted attestation service on top of a binary attestor (here
TPM) still being conform to TCG. We do not elaborate
on this service at this stage due to space restrictions and
only consider the cryptographic proof protocols for proving
the possession of a valid property-certificate conform to the
platform’s configuration.

Note that

confirms the correctness of the correspon-

dence between the platform configuration and certain prop-
erties according to defined criteria. However, following com-
mon practice, such organizations are only liable for inten-
tional misbehavior and not for undetected weaknesses (com-
pare with safety and security tests or common criteria). Par-
ties like

are fully trusted, i.e., by the attestor and the

verifier, since both have to assume that

certifies only

configurations that really have the attested property.

To prevent a flood of desired properties, the involved par-

ties can, e.g., define earmarked property profiles together.
For instance, for end-users one could define a privacy-pro-
tecting Common Criteria [10] protection profile, while con-
tent providers define a content-protecting profile. The TTP
then certifies whether given configurations are compatible
to that protection profiles. If the TTP is a governmental
authority, it can also analyze whether a given platform con-
figuration protects the consumer’s privacy, e.g., by certifying
that it is compatible to privacy laws.

This trusted component could be a service of a trustworthy

operating system.

BUILDING BLOCKS

In this section we introduce the basic terminology and

building blocks used throughout this paper.

Notation.

Let

{

}

ℓ

denote the set of all binary strings of

length

ℓ

which we identify with the integers out of [0; 2

ℓ

A protocol

Prot

() consists of two or more parties, each per-

forming local computations and exchanging messages with
other participants. These parties are modeled as polyno-
mial interactive algorithms. A protocol

Prot

(

) with

the two participants

and

is characterized by the fol-

lowing input and output parameters: The common input

is given to both involved parties

and

, while the private

input

is only available to

, respectively.

When both parties have finished the execution of the proto-
col, each of them obtains its individual output

out

Outputs may include an indicator

ind

∈ {⊤

⊥}

indicating

that the corresponding party accepts/rejects. An execution
(or run) of a protocol is denoted by

(

out

;

out

)

←

Prot

(

;

)

We mark a malicious party, i.e., a party that is controlled
by an adversary, with a

∗

, like

∗

. Note that if the protocol

can be executed by one single party (i.e., non-interactively),
we omit the party’s name.

The proposed PBA scheme makes use of the following

cryptographic primitives:

Signatures.

A digital signature scheme is denoted by a tu-

ple (

GenKey

()

Sign

()

Verify

()) for key generation, signing

and verification algorithms.

With

←

Sign

(

;

) we

mean the signature on a message

signed by the sign-

ing key

. The return value of the verification algorithm

ind

←

Verify

(

;

m, σ

) is a Boolean value

ind

∈ {⊤

⊥}

A certificate on a quantity

with respect to a verification

key

is denoted by

cert

(

;

), a signature generated by

applying the corresponding signing key.

TPM Signatures.

The TPM can create a TPM signature

. The existing TCG technology provides two types of

TPM signatures. The first is DAA signatures [4]. With
a DAA signature, a verifier is convinced that a TPM has
signed a given message, which is either an Attestation Iden-
tity Key (

AIK

) or an arbitrary data string, but the ver-

ifier cannot learn the identity of the TPM. The second is
ordinary RSA-type signatures. A TPM RSA signature is
signed under an

AIK

, which could either be certified by

a Privacy-CA or be introduced by the TPM itself using a
DAA signature. For simplicity, we do not distinguish these
two cases, and denote the private signing key used to create

and denote the corresponding public verification

key used to verify

. We denote the TPM signing

algorithm on a message

←

SignM

(

, m

Commitment Scheme.

We apply the commitment scheme

by Pedersen [24]: Let

com

be the secret commitment key. A

commitment on a message

is computed as

com

mod

is a large prime,

is a generator of a cyclic sub-

group

⊆

∗

of prime order

and

−

is chosen

randomly from

; furthermore, log

(

) is unknown to the

committing party. Both the message

and

com

are taken

from

. The Pedersen commitment scheme as described

above is perfectly hiding and computationally binding under
the discrete logarithm assumption.

CL Signatures.

We apply a variant of the Camenisch and

Lysyanskaya (CL) signature scheme [6], as already used in
[4], for signing a tuple of messages

:= (

, . . . , x

), where

∈ {

}

ℓ

(

= 1

, . . . , m

) and

ℓ

denotes the maximum

binary length for each

. In our specification, the CL sign-

ing algorithm is denoted as (

A, e, v

)

←

Sign

(

;

), where

is an RSA-type private key created from strong primes.

The signature (

A, e, v

) satisfies

≡

. . .

mod

, where the value

∈

ℓ

−

ℓ

−

ℓ

′

−

] is a random

prime, the value

of length

ℓ

is a random integer, and the

tuple (

, . . . , R

, S, Z, n

) is the corresponding public key

. The CL signature verification algorithm is denoted as

ind

←

Verify

(

;

X, A, e, v

In [5], it is remarked that the CL signature has the ability

to be

randomized

. This means that the signature (

A, e, v

)

can be masked to ( ˆ

, e,

−

) with an ar-

bitrary value

. From the verifier’s point of view, ( ˆ

A, e,

)

and (

A, e, v

) are both valid signatures on

Zero-knowledge Proofs of Knowledge.

Zero-knowledge

proofs of knowledge are interactive protocols carried out be-
tween two parties: a prover and a verifier. During such
a protocol run, a verifier is convinced with overwhelming
probability that the prover is aware of some secret and that
a certain predicate related to this secret is true. However,
the verifier does not learn anything beyond this assertion.

Several protocols in this paper will contain some proofs

of knowledge of relations among discrete logarithms under
exponential one-way homomorphisms. To describe the se-
mantics of these proofs we apply the notation suggested by
Camenisch and Stadler [8]. For example,

P K

{

(

α, β

) :

∧

∈

[

a, b

]

}

denotes a zero-knowledge proof of knowledge that a prover
is aware of some secret values

and

such that

holds and, moreover, that

is contained in the interval [

a, b

are elements of some group

with

provided as common input to both parties; this holds for the
integers

and

as well.

Depending on the cryptographic assumption the one-way

property of a given homomorphism is based on

, the

sound-

ness

of the corresponding zero-knowledge proof is valid un-

der the same assumption

Furthermore, all occurring

proofs of knowledge feature the

statistical zero-knowledge

property. In the case where the verifier chooses the chal-
lenge uniformly at random, we obtain a

honest verifier zero-

knowledge

(HVZK) proof of knowledge protocol.

According to the Fiat-Shamir Heuristic [13], such a proof

of knowledge protocol can be transformed into a non-inter-
active signature for a message

which will be denoted as

SP K

{

(

)

}

(

here either strong RSA assumption for CL signatures or the

discrete logarithm assumption for Pedersen’s commitment
scheme

provided that the verifier’s challenge is chosen smaller than

the smallest factor of the underlying group’s order (either

(

) or

)

THE PROPOSED PROTOCOL FOR PBA

In this solution, we describe a concrete property-based at-

testation protocol, which consists of property certificates, a
PBA signing algorithm, a verification algorithm and a re-
vocation check process. This protocol holds the security
properties of

unforgeability

and

unlinkability

. Informally,

unforgeability means that a PBA signature can only be pro-
duced with the involvement of a valid TPM to the actual
platform configuration; unlinkability means that from the
PBA signature and its verification protocol, a verifier is not
able to deduce the specific configuration of the platform.

The basic idea is as follows: the host

proves that there

is a valid link between the conventional binary attestation
signature

, generated by the trusted component (here

the TPM), and the certificate (represented by the signature

) of a certificate issuer

attesting that the configu-

ration specification

provides the property specification

denoted by

. Here, the prover obtains the correspond-

ing certificate

as secret input, and the verifier takes the

public key

of the certificate issuer and the property

specification

as individual input. The prover proves di-

rectly that its configuration complies with the one in the
certificate without showing the certificate.

Note that the revocation process in this protocol does not

involve a trusted party. A prover can convince a verifier
that its configuration is not among a given set of revoked
configurations. It is not necessary for a trusted third party
to provide the set of revoked configurations, which could be
negotiated directly between the prover and verifier.

7.1

Security Parameters

In this section, we enumerate the security parameters

ℓ

(

) used in the PBA protocol specified below with their

required bitlength

ℓ

(160) indicates the size of a configu-

ration value

, while

ℓ

(160) determines the binary length

of a certain property

ℓ

∅

(80) denotes the security pa-

rameter controlling the statistical zero-knowledge property
and

ℓ

(160) is the output length of the hash function used

for the Fiat-Shamir heuristic. For Pedersen’s commitment
scheme, the size of the modulus

is set to

ℓ

(1632) and

the size of the order

of the sub group of

∗

ℓ

. The

parameters

ℓ

and

ℓ

should be chosen such that the dis-

crete logarithm problem in the subgroup of

∗

of order

with

and

being primes such that 2

ℓ

> Q >

ℓ

−

and

ℓ

> P >

ℓ

−

, has acceptable computational difficulty.

Furthermore,

ℓ

(2048) indicates the size of an RSA modu-

lus, while

ℓ

(368) and

ℓ

′

(120) are parameters occurring in

the blinded CL signature scheme. Finally,

ℓ

(2536) is the

size of

, a random value which is part of the certificate.

Moreover, we require the following constraints among the

security parameters:

ℓ

> ℓ

ℓ

∅

+ 2

ℓ

≥

max

{

ℓ

, ℓ

}

+ 2

and

ℓ

≥

ℓ

+ max

{

ℓ

, ℓ

}

ℓ

∅

7.2

Property-Configuration Certificates

An acceptable configuration attestation is certified by a

certificate issuer

. The procedures of key generation, cer-

tificate issuing and verification are described in Figure 2.

We denote the corresponding protocols with

(

, vk

)

←

KeyGen

ℓ

)

←

IssueCertCI

(

, ps

))

and

ind

←

VerifyCertCI

(

, ps

)

, σ

)

7.3

Signing Algorithm

The signature procedure is a protocol among the TPM

and the host

and is presented in Figure 3. As a result of

the protocol, the host will have created a masked signature

PBA

, which is based on a TPM signature

on the mes-

sage

, where

is the commitment to configuration

specification

. From the masked signature, the verifier

will be convinced that the platform has a valid configura-
tion associated with a given property

. The protocol is

denoted by

(

;

PBA

)

←

PBASign

(

;

par

com

, cs

, N

)

where the commitment parameters are

par

com

:= (

g, h, P, Q

)

and the public verification key of certificate issuer

= (

n, R

, R

, S, Z

7.4

Verification Algorithm

The verification protocol (see Figure 4) checks if a given

signature

PBA

is correct, i.e., whether the input to the sign-

ing protocol was a configuration with a valid property cer-
tificate and a correct TPM signature. The protocol is de-
noted by

ind

←

PBAVerify

(

PBA

, σ

PBA

, N

), where

PBA

(

par

com

) is the verification key corresponding

to the signature

PBA

7.5

Revocation Check of a Certificate

If for any reason, e.g., due to system security updates, a

set of configuration specifications becomes invalid, the cor-
responding list will be published (usually by

) so that

possible verifiers can access it.

Suppose that

revoked

{

}

,...,τ

is the set of invalid

configuration specifications, either from a public list or ne-
gotiated between prover and verifier. Then the revocation
check protocol in Figure 5, performed by a host

and a

verifier

, checks whether the configuration which was used

for signing some property is contained in the set of revoked
configurations

revoked

. This protocol is denoted by

(

ind

;

)

←

PBARevoke

(

−

;

, r

;

par

com

, f, C

, CS

revoked

)

where

is the host configuration,

com

is the key for

opening the commitment,

is a generator of

and

is the host’s commitment to the configuration

Technically, this proof is derived from a zero-knowledge

protocol to prove the inequality of two discrete logarithms
presented in [7]. The host shows that the configuration

to which it committed during

PBASign

(), is not equal to

any of the revoked configurations

. To achieve this, he

proves the knowledge of both exponents in the commitment
(i.e.,

and

) and that

(

∀

= 1

, . . . , τ

). To

prove these inequalities, the technique introduced in [7] by
Camenisch and Shoup is used. If

for some

, the

verifier would notice this in step 5e, because in this case he
would get

= 1.

7.6

Rogue TPMs

If a TPM is broken, there must be a possibility to recog-

nize this. In our scheme, the TPM signs the configuration
by using a signing key, usually an AIK. If this AIK has been
signed using a DAA signature, then the tagging will be cov-
ered by the DAA rogue tagging, and a potential verifier can
check this. If other mechanisms such as a Privacy-CA are
used to certify the AIK, then this AIK will be put on re-
vocation lists. In any case, the problem of rogue tagging
corrupted TPMs is out of scope of the PBA protocol.

7.7

Security Analysis

We analyzed the security of the PBA protocol in a formal

model based on the simulatability paradigm, as proposed in
[9] and [26]. The ideal-world specification fulfills the require-
ments

unforgeability

and

unlinkability

– and, according to

the proof, the real-world protocol implements this specifica-
tion. The security proof of DAA [4] uses a similar approach.
We show that the security of the PBA protocol relies on CL
signatures (cf. [6]) and Pedersen commitments (cf. [24]),
which in turn are based on the strong RSA assumption and
the discrete logarithm assumption in the corresponding al-
gebraic structures (see Section 6). We summarize this result
in the following theorem.

Theorem 1

The above protocol implements a secure prop-

erty-based attestation system under the discrete logarithm
assumption and the strong RSA assumption in the random
oracle model.

A formal definition of the PBA security model and the

proof of Theorem 1 is given in the extended version of this
paper

. The basic idea of the proof is to specify an ideal

world, where a trusted party

ensures the security proper-

ties. The protocol is said to be secure if for every (polyno-
mially bounded) adversary in the real world, there exists an
adversary in the ideal world, such that both settings cannot
be distinguished (except with negligible probability). This
is achieved by the introduction of a simulator into the ideal
world that has black-box access to the real-world adversary
and acts as ideal-world adversary. Such a simulator is con-
structed independently from the actual adversary and hence
works for all possible adversaries. Then the proof is con-
cluded by showing that both worlds are indistinguishable.

CONCLUSION AND OUTLOOK

In this paper, we proposed the first cryptographic instan-

tiation of a protocol for property-based attestation based on
the TCG trust model. Our approach is based on the del-
egation principle and uses an offline trusted third party as
issuer for property-configuration certificates. Moreover, a
flexible dealing with the revocation of invalid platform con-
figurations was proposed, where revocation is handled by
a two-party protocol between host and verifier without the
involvement of a trusted third party. Finally, we provided
a proof of security under well-established assumptions in a
formal model using the simulatability paradigm.

A further research topic is the question, how more com-

plex properties can be derived automatically. In practice,
it is difficult to be able to determine or compare proper-
ties enforced by a platform configuration. In the future, im-

http://www.prosecco.rub.de/publication.html

Key generation:

On input 1

ℓ

, create a special RSA modulus

of length

ℓ

where

and

are strong primes.

Choose, uniformly at random,

∈

. Output the public verification key

= (

) and

the secret signing key

. We denote this algorithm with

(

)

←

KeyGen

ℓ

)

Signing algorithm:

Given a property specification

∈ {

}

ℓ

and a set of the corresponding configuration specifi-

cations

∈ {

}

ℓ

with

= 1

, ..., t

. The property certificate on each configuration specification is issued as follows.

On input (

, ps

) with

∈ {

}

ℓ

and

∈ {

}

ℓ

, choose a random prime number

of length

ℓ

≥

max(

ℓ

, ℓ

)+2,

and a random number

of length

ℓ

+ max(

ℓ

, ℓ

) +

ℓ

∅

. Compute the value

such that

≡

mod

. The signature on the message (

, ps

) is the tuple

:= (

, e

, v

). We denote this algorithm with

←

IssueCertCI

(

))

Verification algorithm:

Let

∈ {

, ..., t

}

. To verify that the tuple (

, e

, v

) is a signature on message (

, ps

), check

that

≡

mod

, and check that 2

ℓ

> e

ℓ

−

. We denote this algorithm with

ind

←

VerifyCertCI

(

, ps

)

, σ

)

Figure 2: Issuing a Certificate of a Property and Configuration Map.

Players:

TPM

and the corresponding Host

TPM’s input:

;

Host’s input:

:= (

, e

, v

Common input:

= (

n, R

, R

, S, Z

)

par

com

:= (

g, h, P, Q

) ,

(nonce provided by the verifier).

1. The TPM performs as follows

(a) Choose a random

∈

{

}

ℓ

∅

(b) Choose a random

∈

{

}

ℓ

and compute the commitment

mod

SignM

(

par

com

(d) Send to host

with the values

and

2. The host performs the following steps to finish the proof:

(a) Choose at random

∈ {

}

ℓ

(b) Compute ˆ

mod

and ˆ

−

= ( ˆ

A, e

3. The host computes the signature of knowledge protocol

SP K

{

(

, e

v, r

) :

Z/R

≡ ±

(mod

)

∧

(mod

)

∈ {

}

ℓ

∅

ℓ

∧

(

−

ℓ

)

∈ {

}

ℓ

′

ℓ

∅

ℓ

}

(

, N

)

in the following steps:

(a) Computes

′

Z/R

mod

(b) Pick random integers

∈

{

}

ℓ

∅

ℓ

, r

∈

{

}

ℓ

′

ℓ

∅

ℓ

, r

∈

{

}

ℓ

∅

ℓ

, r

∈

{

}

ℓ

∅

ℓ

′

:= ˆ

mod

and ˜

mod

(d) Compute

Hash

(

par

′

(e) Compute

(

−

ℓ

−

) and

over the integers.

(f) The PBA signature will be

PBA

:= ( ˆ

A, σ

, N

, C

, c, s

, s

Figure 3: The PBA Signing Algorithm.

Players:

Verifier

;

Verifier’s input:

, vk

par

com

, ps, σ

PBA

, N

. The verifier verifies the signature by performing as follows:

1. Verify

w.r.t.

on the message (

par

com

). If positive go to the next step.

2. Compute ˆ

′

′−

ℓe

−

mod

and ˆ

−

mod

3. Verify that

Hash

(

par

′

∈ {

}

ℓ

∅

ℓ

and

∈ {

}

ℓ

′

ℓ

∅

ℓ

Figure 4: The Verification Protocol.

Players:

Host

and Verifier

Common input:

(

par

com

, f, C

, CS

revoked

), where

par

com

:= (

g, h, P, Q

) and

revoked

{

}

,...,τ

;

Host’s input:

(

, r

1. The host and verifier compute

(mod

) (

= 1

, ..., τ

2. The host computes

(mod

) and sends

to the verifier.

3. The host randomly picks

∈ {

}

ℓ

, computes

rβ

−

(mod

)(

= 1

, ..., τ

) and sends

to verifier.

4. The host computes the signature of knowledge by performing as follows:

SP K

{

(

, r, α, β

) :

(mod

)

∧

(mod

)

∧

1 =

−

∧

−

for

= 1

, ..., τ

}

(a) Pick random integers

∈

{

}

ℓ

∅

ℓ

, r

∈

{

}

ℓ

∅

ℓ

, r

∈

{

}

ℓ

∅

ℓ

, r

∈

{

}

ℓ

∅

ℓ

(b) Compute ˜

mod

, ˜

mod

, ˜

−

mod

and ˜

−

for

= 1

, ..., τ

Hash

(

...

(d) Compute

and

. (Note that

mod

(e) Send the signature

:= (

c, s

, s

) to the Verifier.

5. The verifier verifies the signature as follows:

(a) Verify that

∈ {

}

ℓ

∅

ℓ

(b) Compute ˆ

mod

−

mod

and

−

c
j

mod

(

∀

= 1

, ..., τ

Hash

(

...

(d) If ˆ

, accept the proof, otherwise reject the proof.

(e) If

= 1 holds for

= 1

, ..., τ

was not committed to any of

(

= 1

, ..., τ

), the verifier accepts

Figure 5: The Revocation Check Protocol.

proved software-engineering methods based on formal meth-
ods, proof-carrying code and semantic code analysis may
give the chance to formally or semi-formally derive proper-
ties from code directly and thus to prevent the need for a
trusted third party.

REFERENCES

[1] W. A. Arbaugh, D. J. Farber, and J. M. Smith. A secure and

reliable bootstrap architecture. In

Proceedings of the IEEE

Symposium on Research in Security and Privacy

, pages

65–71, Oakland, CA, May 1997, IEEE Computer Society Press.

[2] P. Barham, B. Dragovic, K. Fraser, S. Hand, T. Harris, A. Ho,

R. Neugebauer, I. Pratt, and A. Warfield. Xen and the art of
virtualization. In

SOSP ’03: Proceedings of the 19th ACM

symposium on Operating systems principles

, pages 164–177,

New York, NY, USA, 2003. ACM Press.

[3] P. Barham, B. Dragovich, K. Fraser, S. Hand, A. Ho, and

I. Pratt. Safe hardware access with the Xen virtual machine
monitor. In

1st Workshop on Operating System and

Architectural Support for On-Demand IT Infrastructure

2004.

[4] E. Brickell, J. Camenisch, and L. Chen. Direct anonymous

attestation. In

Proceedings of the 11th ACM Conference on

Computer and Communications Security

, Washington, DC,

USA, Oct. 2004. ACM Press.

[5] J. Camenisch and J. Groth. Group signatures: Better efficiency

and new theoretical aspects. In C. Blundo and S. Cimato,
editors,

SCN

, volume 3352 of

LNCS

, pages 120–133. Springer,

2004.

[6] J. Camenisch and A. Lysyanskaya. A signature scheme with

efficient protocols. In

Third Conference on Security in

Communication Networks - SCN ’02

, volume 2576 of

LNCS

pages 268–289. Springer-Verlag, Berlin Germany, 2002.

[7] J. Camenisch and V. Shoup. Practical verifiable encryption

and decryption of discrete logarithms. In D. Boneh, editor,

CRYPTO

, volume 2729 of

Lecture Notes in Computer

Science

, pages 126–144. Springer, 2003.

[8] J. Camenisch and M. Stadler. Proof systems for general

statements about discrete logarithms. Technical Report TR
260, Department of Computer Science, ETH Z¨

urich, Mar. 1997.

[9] R. Canetti. Security and composition of multiparty

cryptographic protocols.

Journal of Cryptology

13(1):143–202, Winter 2000.

[10] Common Criteria Project Sponsoring Organisations.

Common

Criteria for Information Technology Security Evaluation

Aug. 1999. Version 2.1, adopted by ISO/IEC as ISO/IEC
International Standard (IS) 15408 1-3. Available from

http://csrc.ncsl.nist.gov/cc/ccv20/ccv2list.htm

[11] J. Dyer, M. Lindemann, R. Perez, R. Sailer, L. van Doorn,

S. W. Smith, and S. Weingart. Building the IBM 4758 Secure
Coprocessor.

IEEE Computer

, 34(10):57–66, 2001.

[12] P. England, B. Lampson, J. Manferdelli, M. Peinado, and

B. Willman. A trusted open platform.

IEEE Computer

36(7):55–63, 2003.

[13] A. Fiat and A. Shamir. How to prove yourself: Practical

solutions to identification and signature problems. In A. M.
Odlyzko, editor,

Advances in Cryptology – CRYPTO ’86

volume 263 of

LNCS

, pages 186–194, Santa Barbara, CA,

USA, 1987. International Association for Cryptologic Research,
Springer-Verlag, Berlin Germany.

[14] T. Garfinkel, B. Pfaff, J. Chow, M. Rosenblum, and D. Boneh.

Terra: a virtual machine-based platform for trusted computing.
In

Proceedings of the 19th ACM Symposium on Operating

Systems Principles (SOSP’03)

, pages 193–206, 2003.

[15] T. C. Group. TCG software stack specification.

http://trustedcomputinggroup.org

, Aug. 2003. Version 1.1.

[16] V. Haldar, D. Chandra, and M. Franz. Semantic remote

attestation: A virtual machine directed approach to trusted
computing. In

USENIX Virtual Machine Research and

Technology Symposium

, May 2004. also Technical Report No.

03-20, School of Information and Computer Science, University
of California, Irvine; October 2003.

[17] D. Lie, C. A. Thekkath, and M. Horowitz. Implementing an

untrusted operating system on trusted hardware. In

Proceedings of the 19th ACM Symposium on Operating
Systems Principles (SOSP’03)

, pages 178–192, 2003.

[18] R. MacDonald, S. Smith, J. Marchesini, and O. Wild. Bear:

An open-source virtual secure coprocessor based on TCPA.

Technical Report TR2003-471, Department of Computer
Science, Dartmouth College, 2003.

[19] J. Marchesini, S. Smith, O. Wild, A. Barsamian, and

J. Stabiner. Open-source applications of TCPA hardware. In

20th Annual Computer Security Applications Conference

ACM, Dec. 2004.

[20] J. Marchesini, S. W. Smith, O. Wild, and R. MacDonald.

Experimenting with TCPA/TCG hardware, or: How I learned
to stop worrying and love the bear. Technical Report
TR2003-476, Department of Computer Science, Dartmouth
College, 2003.

[21] Microsoft Corporation. Building a secure platform for

trustworthy computing. White paper, Microsoft Corporation,
Dec. 2002.

[22] C. Mundie, P. de Vries, P. Haynes, and M. Corwine. Microsoft

whitepaper on trustworthy computing. Technical report,
Microsoft Corporation, Oct. 2002.

[23] G. C. Necula and P. Lee. The design and implementation of a

certifying compiler. In

Proceedings of the 1998 ACM

SIGPLAN Conference on Prgramming Language Design and
Implementation (PLDI)

, pages 333–344, 1998.

[24] T. P. Pedersen. Non-interactive and information-theoretic

secure verifiable secret sharing. In J. Feigenbaum, editor,

Advances in Cryptology – CRYPTO ’91

, volume 576 of

LNCS

, pages 129–140. International Association for

Cryptologic Research, Springer-Verlag, Berlin Germany, 1992.
Extended abstract.

[25] B. Pfitzmann, J. Riordan, C. St¨

uble, M. Waidner, and

A. Weber. The PERSEUS system architecture. Technical
Report RZ 3335 (#93381), IBM Research Division, Zurich
Laboratory, Apr. 2001.

[26] B. Pfitzmann and M. Waidner. A model for asynchronous

reactive systems and its application to secure message
transmission. In

Proceedings of the IEEE Symposium on

Research in Security and Privacy

, pages 184–200, Oakland,

CA, May 2001, IEEE Computer Society Press.

[27] J. Poritz, M. Schunter, E. Van Herreweghen, and M. Waidner.

Property attestation—scalable and privacy-friendly security
assessment of peer computers. Technical Report RZ 3548, IBM
Research, May 2004.

[28] A.-R. Sadeghi and C. St¨

uble. Taming “trusted computing” by

operating system design. In

Information Security

Applications

, volume 2908 of

LNCS

, pages 286–302.

Springer-Verlag, Berlin Germany, 2003.

[29] A.-R. Sadeghi and C. St¨

uble. Property-based attestation for

computing platforms: Caring about properties, not
mechanisms. In

The 2004 New Security Paradigms

Workshop

, Virginia Beach, VA, USA, Sept. 2004. ACM

SIGSAC, ACM Press.

[30] D. Safford. Clarifying misinformation on TCPA. White paper,

IBM Research, Oct. 2002.

[31] D. Safford. The need for TCPA. White paper, IBM Research,

Oct. 2002.

[32] R. Sailer, T. Jaeger, E. Valdez, R. Caceres, R. Perez,

S. Berger, J. L. Griffin, and L. van Doorn. Building a
MAC-based security architecture for the Xen open-source
hypervisor. In

ACSAC ’05: Proceedings of the 21st Annual

Computer Security Applications Conference

, pages 276–285,

Washington, DC, USA, 2005. IEEE Computer Society.

[33] R. Sailer, E. Valdez, T. Jaeger, R. Perez, L. van Doorn, J. L.

Griffin, and S. Berger. sHype: Secure hypervisor approach to
trusted virtualized systems. Research Report RC23511, IBM
T.J. Watson Research Center, Yorktown Heights, NY, USA,
Feb 2005.

[34] R. Sailer, X. Zhang, T. Jaeger, and L. van Doorn. Design and

implementation of a TCG-based integrity measurement
architecture. In

Proceedings of the 13th USENIX Security

Symposium

. USENIX, Aug. 2004.

[35] Trusted Computing Group. TPM main specification. Main

Specification Version 1.2 rev. 85, Trusted Computing Group,
Feb. 2005.

[36] Trusted Computing Platform Alliance (TCPA). Main

specification, Feb. 2002. Version 1.1b.